Formal validation of the Arm v8-M specification

ARM logo In my last post about natural language specifications, I talked about the problem with executable specifications: they are great for specifying existing behaviour but they are bad about describing overall properties and, in particular, what is not allowed to happen. This makes it possible that extensions that add new behaviour could break fundamental properties of the specification without anybody noticing.

My solution was to revisit some of the English prose in Arm’s architecture specification manual that states invariants and cross-cutting properties about security, exceptions, etc. This post talks about how we can verify these properties and some of what I found when I applied my tools to the v8-M specification of Arm’s microcontrollers.

(This post is based on some of the ideas in my forthcoming OOPSLA 2017 paper “Who guards the guards? Formal Validation of the Arm v8-M Architecture Specification”.)

How to prove properties of specifications

There are two ways that you can mechanically prove that something is true. The first is the way we learned to prove things in school or university: by making a series of logical arguments involving rules of arithmetic, logic, etc. This is a very powerful approach that (ignoring Gödel) can prove anything you want to prove. The only downsides are that it is very hard work and that it requires a lot of practice to learn how to write these proofs.

The other way is to use a black box tool like a SAT Solver, an SMT Solver or a model checker that can prove the property for me without requiring me to detail every step. Since the computer is doing all the work, these tend to be more computationally expensive but, thanks to a combination of Moore’s Law and better algorithms, they are fast enough to be useful. The upside of these solvers is that they require much less expertise to use them so they are much easier to deploy in an industrial setting. One other important property of using these black box solvers that is useful is that when they find that a property is not true, they provide a counterexample: a set of inputs for which the property is not true. These counterexamples are incredibly useful because it gives me a familiar debug experience: system fails for input X, let’s figure out why.

The major downside is that they can’t prove everything. There are two sides to this. The first is that they run out of memory or get stuck trying the wrong way to solve some problem and, because they are a black box, it is not always clear how you can help them.

The other limitation is that they can basically only answer one question: is there an input X such that property P holds?

∃ X. P

Although, since the tool can definitively tell you “no, there is no such X”, you can interpret a “no” answer as a proof of this property

∀ X. ¬ P

So my task was easy: convert properties written in ASL into SMT expressions. How hard could that be?

Converting ASL to SMT

ASL is quite a rich language: it has function calls, assignments, if-statements, for-loops, while loops, polymorphism, dependent types, exceptions, arithmetic operations, logical operators, arrays, etc. SMT is a pure expression language: it has arithmetic operations, logical operators and arrays and nothing else. So to convert ASL to SMT, all I have to do is remove every convenient programming feature and turn the entire thing into a giant, unstructured expression.

Fortunately, I had previously had to figure out how to turn ASL into Verilog. Verilog is more expressive than SMT but not by much so I could reuse many of the same transformations. For example, to get rid of polymorphism and dependent types, I use two transformations: specialization and monomorphization.

Specialization

Specialization is used to simplify calls to polymorphic functions. Suppose I have an instruction that performs a SIMD addition on two registers and it can split the registers into either 8, 16, 32 or 64-bit elements where the element size is determined by a 2-bit field called SZ in the instruction encoding. The instruction definition might look like this:

integer sz = 8 << UInt(SZ); // calculate element size
V[d] = Add_SIMD(V[m], V[n], sz)

This is tricky because the function Add_SIMD is going to work on elements of different sizes. The way I can eliminate this is by performing a case-split on the variable SZ:

case SZ of
    when '00' V[d] = Add_SIMD(V[m], V[n], 8)
    when '01' V[d] = Add_SIMD(V[m], V[n], 16)
    when '10' V[d] = Add_SIMD(V[m], V[n], 32)
    when '11' V[d] = Add_SIMD(V[m], V[n], 64)

Now each call to Add_SIMD operates on a different element width, which sets us up for the next step in the transformation.

Monomorphization

Monomorphization is used to simplify polymorphic functions based on the different calls to the function within the specification. For example, consider the Add_SIMD function that is used above.

Add_SIMD splits two N-bit values into smaller chunks of length sz, adds corresponding chunks from the two inputs and returns the result.

bits(N) Add_SIMD(bits(N) x, bits(N) y, integer sz)
    assert N MOD sz == 0;
    integer elements = N DIV sz;
    bits(N) result;
    for i = 0 to elements - 1 do
        result[i*sz +: sz] = x[i*sz +: sz] + y[i*sz +: sz];
    return result;

To monomorphize this, I create a separate version for each value of N and of sz that is used in the specification. For example, for 128-bit values split into 32-bit chunks, I get this version of the function.

bits(128) Add_SIMD_128_32(bits(128) x, bits(128) y)
    bits(128) result;
    for i = 0 to 3 do
        result[i*32 +: 32] = x[i*32 +: 32] + y[i*32 +: 32];
    return result;

And I then unroll all the loops to get this

bits(128) Add_SIMD_128_32(bits(128) x, bits(128) y)
    bits(128) result;
    result[0  +: 32] = x[0  +: 32] + y[0  +: 32];
    result[32 +: 32] = x[32 +: 32] + y[32 +: 32];
    result[64 +: 32] = x[64 +: 32] + y[64 +: 32];
    result[96 +: 32] = x[96 +: 32] + y[96 +: 32];
    return result;

After simplifying the types, I work on eliminating function calls, if-statements and assignments. The easy one is function calls: all I have to do is inline every function.

If-conversion

If-statements and assignments are also quite easy: I use a variant of the classic “if-conversion” transformation used in vectorizing compilers. For example, if I have this code:

integer x;
integer y;
if c then
    x = 1;
    y = 64;
else
    x = 2;
    y = 32;

then I convert it to this code instead

integer x = if c then 1 else 2;
integer y = if c then 64 else 32;

So all I have to do is repeat that transformation systematically across the entire specification.

Converting to SMT

Repeating the above for the entire architecture specification results in a single giant function that consists entirely of statements of the form

<type> <variable> = <expression>;

And, once I have that, all I have to do is convert ASL expression syntax to SMT expression syntax. For example, the statement:

integer x = a + b + 1;

is converted to

(define-const x Int (+ a (+ b 1)))

The final result

As you might imagine, the result of specializing all instructions, monomorphizing all functions, unrolling all loops, inlining all functions and if-converting all conditionals is quite large. It turns the 15,000 line v8-M specification into approximately 500,000 lines of SMT.

My favourite solver is the Z3 SMT solver developed by Leonardo de Moura and Nikolaj Bjørner. Thanks to some incredibly good engineering by them and their colleagues at Microsoft Research, Z3 can easily cope with ridiculously large inputs like the one that I generate.

Proving properties

So now I have some properties (see my previous post) and I have a way to convert ASL to SMT problems. So it is time to try to prove something.

I have a total of 38 invariants and 23 properties and I want to show two things:

After taking a cold reset (i.e., a power-on reset), all of the invariants hold.
If all the invariants hold before the processor takes a step then all of the invariants and all of the properties hold afterwards.

Let’s start with the simplest configuration of the v8-M specification: with the security features of TrustZone for M-class disabled. At the moment, I can prove that all of the invariants hold after reset and that 36 of the invariants hold and 21 of the properties hold. What about the other 4? One of the properties does not hold. Either there is a bug in the property or there is a bug in the specification — I am not sure which and need to spend more time debugging it. The proofs of two of the invariants and one of the properties are timing out: they might be true, they might be false, I can’t tell at the moment. My main worry here is the invariants because if they are not true, then any proofs that depend on them are not sound. So, for now, I can use this as a tool for finding bugs but I can’t claim that the properties are all guaranteed to hold.

The usual way to show how fast your tool is at proving a set of properties is to plot a graph that shows how long it takes to prove 10%, 20%, … 100% of all the properties. In the paper I wrote about this work, I split the sets of properties and invariants up into several different categories so this graph from the paper has several lines in it (that I won’t explain here). The main thing to notice is that proofs involving reset do not take very long (because the reset code has very few choices in it) and that proofs about the transition function take between a second and 1000 seconds with most of them proved in around 100 seconds.

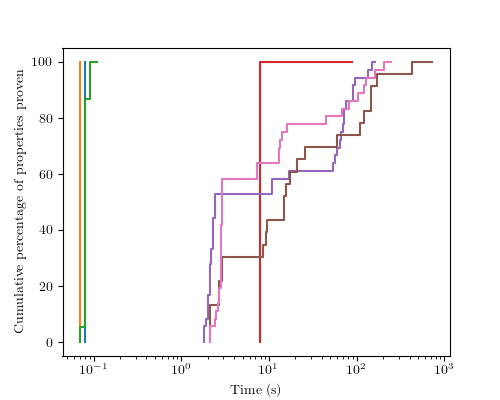
Cumulative solution time for Non-Secure configuration of v8-M properties

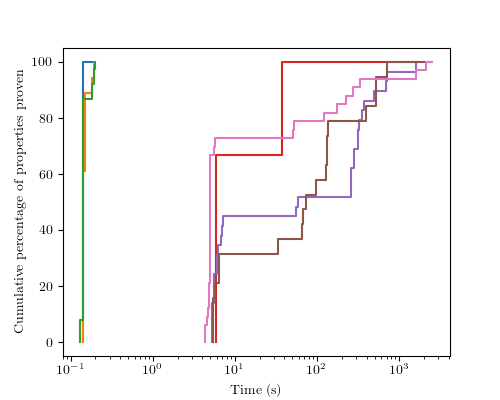
And what if I enable TrustZone for M-class? The SMT translation grows to around 750,000 lines of SMT, and I am able to prove 33 invariants and 19 properties. Again, I can prove that all the invariants hold after reset and this time, I have 2 failing properties that I need to debug and I have 5 invariants and 2 properties that are timing out. Again, this is not perfect, but it is good enough that I was able to find more bugs so, for now, it is a great way of improving the quality of the specification.

With the larger size and the ability of the processor to be in either NonSecure mode or Secure mode, the proof time goes up. Again, reset properties are proved very quickly but the proofs are between 3 and 10 times slower.

Cumulative solution time for Secure configuration of v8-M properties

Of course, the whole point of all this work was to find bugs in the specification. All this work has found 12 bugs so far (in a specification that had already been very thoroughly tested) and I am nowhere near writing all the properties that I think should hold for the specification.

Summary

In my last post about natural language specifications, I talked about the possibility of bugs in an architecture specification that would not be caught by testcases no matter how thorough those tests might be and the need for a meta-specification that specifies cross-cutting properties and invariants of the specification itself. I also talked about mining the English prose in the Arm Architecture Reference Manual for those properties and how I could formalize them. This post finishes the story by describing how I could use SMT checkers to prove that the properties hold and, more importantly, to find bugs in the specification.

If you want to read more about this, you might want to read my forthcoming OOPSLA 2017 paper “Who guards the guards? Formal Validation of the Arm v8-M Architecture Specification” that describes the meta-specification language, the properties and the results in more detail.

As a bit of a teaser, let me point out that one thing you can do with an SMT solver is to prove universally quantified properties as I do here. But there are lots of other interesting things they can be used for…

Written on September 24, 2017.
The opinions expressed are my own views and not my employer's.